Suppose a system uses a constant internal initialization vector to encrypt/decrypt data in CBC mode, and you'd like to know what it is. If you can make the system decrypt chosen ciphertexts, this is how you do it:

1. Make the system decrypt two equal blocks of ciphertext (e.g. all zeroes).
2. XOR the two resulting blocks of "plaintext" together.
3. XOR that with the original ciphertext block.

Visually:

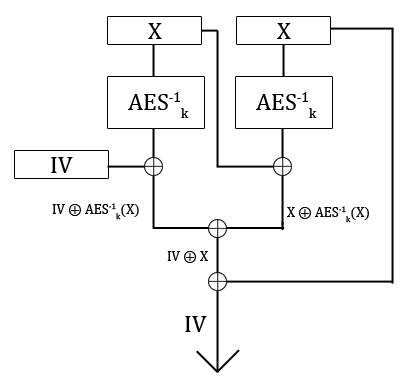
The best I can think of for recovering a static IV under chosen plaintext is a meet-in-the-middle attack as follows.

Observation 1: We can specify input directly to the cipher by:

1. Encrypt a one-block plaintext X, getting the resulting ciphertext C.
2. Encrypt the two-block plaintext X||(Y xor C), where Y is the block we want to feed directly into the cipher.
3. The second block of ciphertext will be the result of feeding Y directly into the cipher.

Observation 2: We can encrypt the IV itself and variations of it by varying the first block of plaintext. Formally C = E(V xor IV), when V is the first block of plaintext. We'll call V a "variation vector."

So,

1. Create a lookup table mapping 2^64 (assuming the block size is 128 bits) random variation vectors from the resulting ciphertext. This lets us look up what variation we made to the IV to result in a given ciphertext block.
2. Use the method in observation 1 to encrypt random blocks fed directly into the cipher. Look up each ciphertext in the table from step (1). If it's there, then the IV is <the block that was fed directly into the cipher> XOR <the variation vector>

The lookup table from step (1) gives us a 1 in 2^64 chance of finding the IV per known plaintext-ciphertext pair. So it should take about 2^64 iterations in step (2) before we recover the IV.