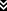244

Centripetal Acceleration

A mass M is connected by a string of length r to a point C. The mass is orbiting C in a circle with a constant tangential velocity v. What is the radial acceleration a of the mass?

The well-known equation for the acceleration is a = v2/r. It's usually derived by taking the second derivative of the mass's position vector with respect to time.

I worked out a different way to do it, which involves only basic geometry and the average value of sin(x) from 0 to π. We find the centripetal force by the following process:

  1. Use a simple method to find the average value of some function f. For this problem, f is the force in the y direction.
  2. Write f in terms of some unknown x. For this problem, x is the radial force.
  3. Equate the two averages to solve for x.

I suspect this process will prove useful for solving other problems as well. Let's see how we can use it to solve the centripetal acceleration problem.

Consider two snapshots of the rotating system at times t0 and t1.

t0
t1

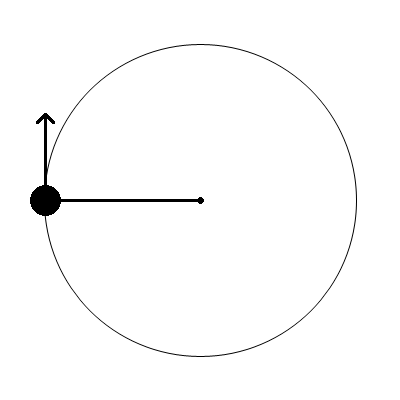
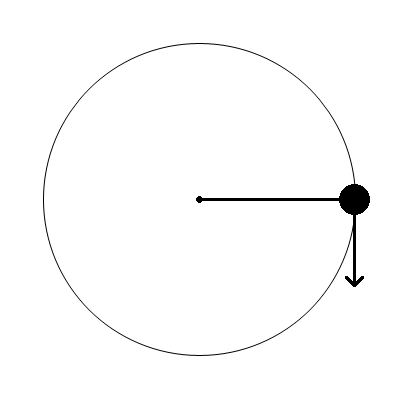
At t0, the mass's momentum is completely in the y direction. There is no x component to the momentum. At t1, half a revolution later, the momentum is in the exact opposite direction.

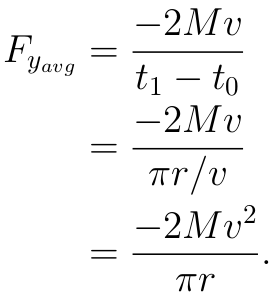
If the momentum at time t0 is Mv and the momentum at time t1 is M(-v), then the total change in momentum is -Mv - Mv = -2Mv. We can get the average rate of change of the momentum in the y direction by dividing by the time. Since the force in the y direction is the rate of change of momentum in the y direction, this is also equal to the average force in the y direction.

Okay, that tells us the average force in the y direction, but that's not the force we want. We want the radial force.

But look! We know how to write the force in the y direction as a function of the radial force. If the radial force is Fs and θ is the angle the string makes with the y axis, then:

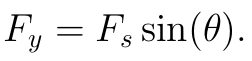
So the average of Fssin(θ) over the half-circle of motion will be equal to the average of Fy, which we already know as Fyavg!

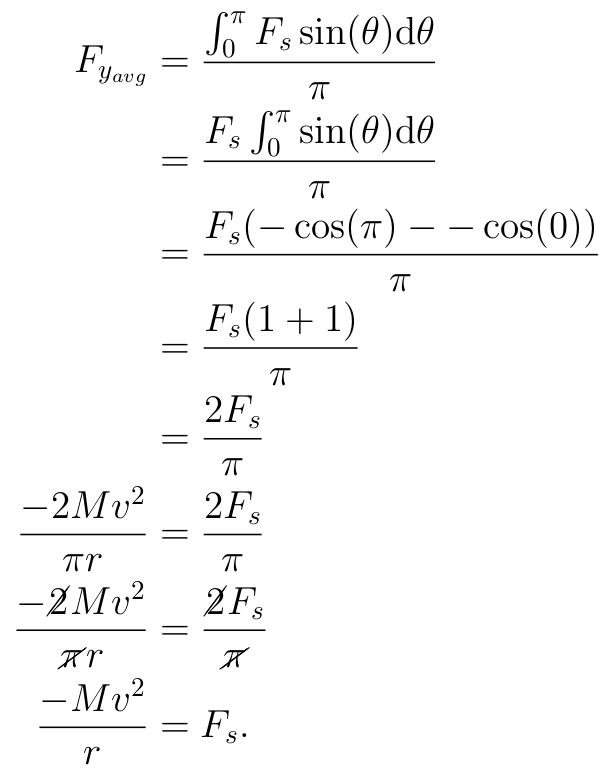
That's it! The radial force Fs is -Mv2/r. Then, since F=Ma, the radial acceleration is a = -v2/r. It is negative because it is in the downward direction when Fy is at its maximum. If we are only interested in the magnitude, then a = v2/r.