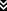The New York Times and Algebra
The New York Times recently put out an article titled "The Interview Brings In $15 Million on Web". In the story, they mention the movie generated "$15 million in online sales" from "about two million transactions" composed of "$6 digital rentals" and "$15 sales."
The writers wondered how many of the transactions were rentals and how many were sales, saying, "Sony did not say how much of that total represented $6 digital rentals versus $15 sales."
This prompted Dan Meyer to tweet the following image:
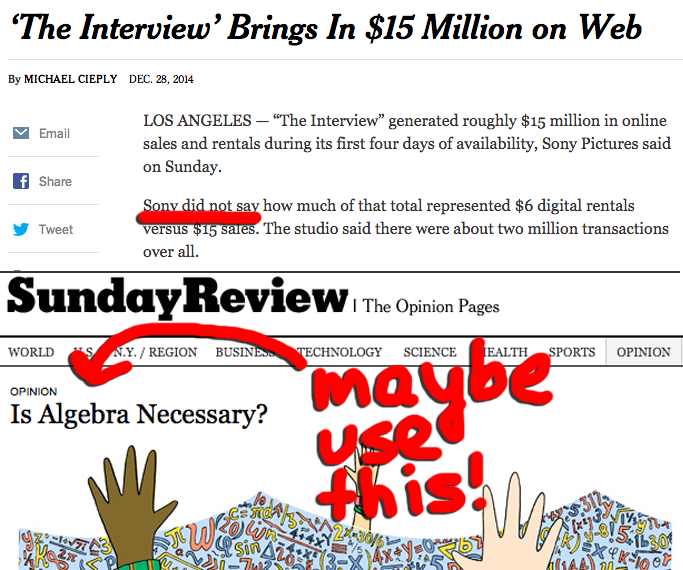
The image criticizes the New York Times for not being able to figure out the solution with algebra, pointing to the headline of an opinion piece titled "Is Algebra Necessary?" On Dan's blog, he puts the figures into a linear equation solver and comes up with 1,666,667 rentals and 333,333 sales, a ratio of 5 to 1.
While it may be worthwhile to criticize a New York Times writer for not valuing algebra, Dan's analysis is wrong. The solution he gives is only one of many possible solutions, with very different rentals to sales ratios!
To see why, we are going to create two alternate universes. We will make sure the New York Times gets the exact same information in both universes, so that there's no way for them to know which universe they are in. The first universe will be crafted so that the rentals to sales ratio is very high, and the second universe will be made so the ratio is close to 1. Since both universes "look the same" to the New York Times, this shows that they can't possibly tell, given the information, what the actual ratio is.
Here are the two universes:
Universe 1:
- There are 2,399,990 rentals and 11,111 sales.
- In total, there are 2,411,101 transactions (2,399,990 + 11,111)
- In total, Sony gets $14,566,605 ($6 * 2,399,990 + $15 * 11,111)
- The ratio of rentals to sales is 216 to 1 (2,399,990 / 11,111)
- Sony rounds the figures to the nearest million and tells the New York Times, "There were 2 million transactions worth $15 million. Rentals were $6 and sales were $15."
Universe 2:
- There are 1,011,110 rentals and 588,889 sales.
- In total, there are 1,599,999 transactions (1,011,110 + 588,889)
- In total, Sony gets $14,899,995 ($6 * 1,011,110 + $15 * 588,889)
- The ratio of rentals to sales is 1.72 to 1 (1,011,110 / 588,889)
- Sony rounds the figures to the nearest million and tells the New York Times, "There were 2 million transactions worth $15 million. Rentals were $6 and sales were $15."
Notice that in both universes, the New York Times gets the exact same information. Therefore, from the information they are given, the New York Times cannot know whether they are in Universe 1 or Universe 2. In Universe 1, the ratio is 216, and in Universe 2, the ratio is 1.72. Therefore, the New York Times have no way to know whether the ratio is 216 or 1.72. This is two orders of magnitude of uncertainty.
Of course, Universe 1 and Universe 2 aren't the only possible universes, but that doesn't matter to the point we're making, since having more universes only adds to the uncertainty and makes the New York Times' job harder.
So, supposing Sony didn't give the New York Times the exact figures, they had no way of approximating the correct ratio. If the New York Times did get the exact figures, without any rounding, then Dan's method of solving the linear equation would have worked. But, given the article's text, we have no reason to believe the New York Times had access to the exact figures, and, as shown above, the rounding destroys almost all information about the ratio.
This all goes to show that it's important to understand how to use math, and not just to do math. It's one thing to be able to solve for the sides of a triangle, solve systems of linear equations, and compute integrals. It's a whole different thing to know when those tools can (and can not) be applied to real-world problems.